\[x\]
inscribed in an isosceles triangle of height \[h\]
and base angle \[\alpha\]
.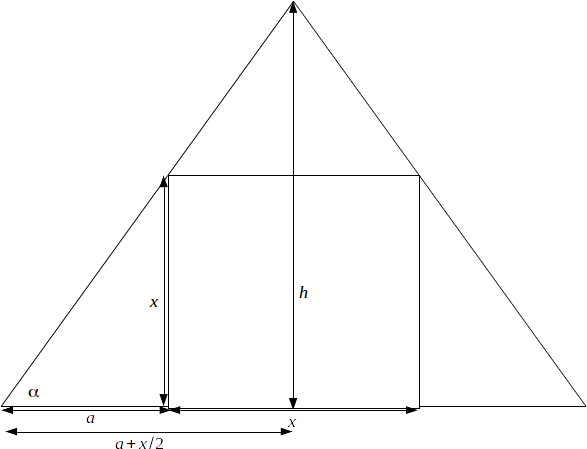
\[tan \alpha = \frac{x}{a}\rightarrow a= \frac{x}{\tan \alpha}\]
Also
\[tan \alpha = \frac{h}{a+ x/2} = \frac{h}{x/tan \alpha + x/2}= \frac{2h tan \alpha}{2x+ xtan \alpha}\]
From the last equation,
\[1=\frac{2h}{2x+ xtan \alpha} \rightarrow x(2+ tan \alpha) =2h \rightarrow x= \frac{2h}{2+ tan \alpha}\]
