Is it possible to construct a triangle with a 60 degree angle with sides in an arithmetic progression? If so, then the smallest side must be opposite the smallest angle, and the largest side opposite the largest angle. We obtain the triangle below.
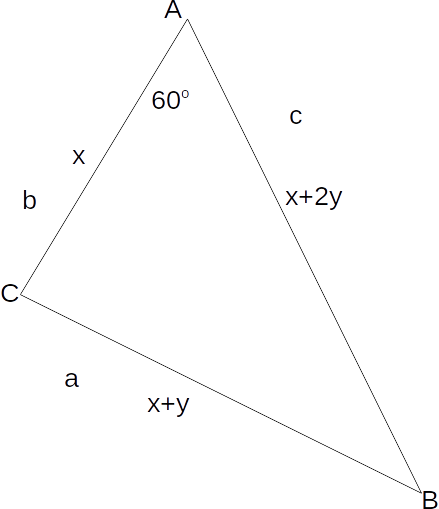
\[a^2 = b^2+c^2-2 \times b \times c \times cos A\]
\[(x+y)^2 = x^2+(x+2y)^2-2 \times x \times (x+2y) \times cos 60\]
\[(x+y)^2 = x^2+(x+2y)^2-2x(x+2y)cos 60\]
\[x^2+2xy+y^2 = x^2+x^2+4xy+4y^2-2x(x+2y) \times \frac{1}{2}\]
\[ x^2+2xy+y^2 = x^2+x^2+4xy+4y^2-x^2-2xy\]
\[0 = 3y^2 \]
Hence
\[y=0\]
.All the sides are length
\[x\]
units and the triangle is isosceles, so no such triangle exists. 