Is it possible to construct a triangle with a 60 degree angle with sides in a Geometric Progression? If so, then the smallest side must be opposite the smallest angle, and the largest side opposite the largest angle. We obtain the triangle below.
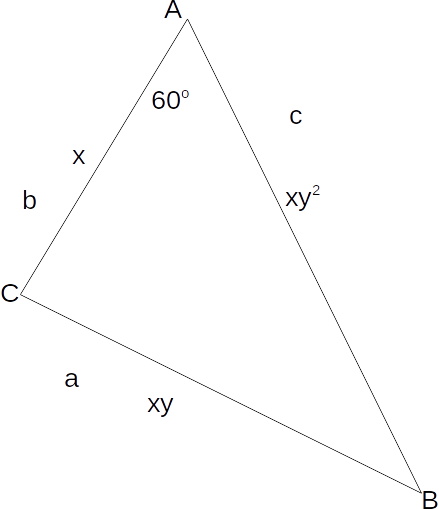
\[a^2 = b^2+c^2-2 \times b \times c \times cos A\]
\[(xy)^2 = x^2+(xy^2)^2-2 \times x \times (xy^2) \times cos 60\]
\[(xy)^2 = x^2+(xy^2)^2-2x(xy^2)cos 60\]
\[x^2y^2 = x^2+x^2y^4-2x(xy^2) \times \frac{1}{2}\]
\[ x^2y^2 = x^2+x^2y^4-x^2y^2\]
\[y^2 = 1+y^4-y^2\]
\[ 0 = y^4-2y^2+1\]
\[0= (y^2-1)^2\]
Hence
\[y=1\]
.All the sides are length
\[x\]
units and the triangle is isosceles, so no such triangle exists. 