It is very easy to solve linear inequalities of the form
almost as easy as solving linear equations:
Solving an absolute inequality, where the equation includes modulus signs is a little bit trickier. When we remove the minus sign it can be hard to work out which way the inequality signs point. Given this, the safest way to solve these equations is either to sketch both absolute functions so that you can see graphically which way the modulus signs point, or square both sides, making both sides positive even without the need for the modulus brackets, then factorising and solving the resulting quadratic inequality.
Example: Solve
Squaring both sides gives
We expand the brackets and simplify to give
Now move every term to the right hand side to give
We can divide by the common factor non zero 3 to obtain
The quadratic factorises to give
The graph
is illustrated below.
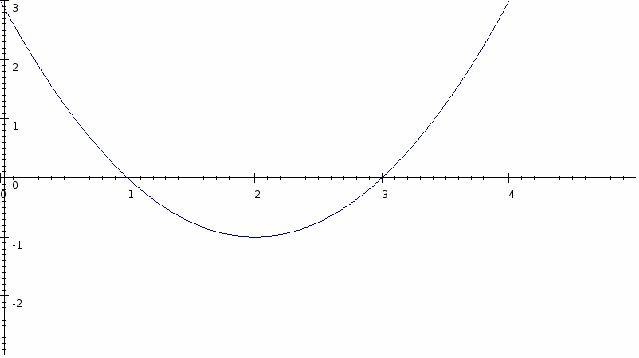
We want those values of
for which
ie
hence the set of values ofsatisfying
is given by
If instead the question had asked to solve
we would have had solved
so that
or
Notice that now the set ofconsists of two intervals.