Graph - A visual representation of a set X of objects and relationships. Each member of X is represented as a vert ex or node. Relationships are represented by edges or arcs.
Vertex or Node - A point representing a member of the set.
Edge or Arc - A link between vertices. An edge must have a vertex at each end.
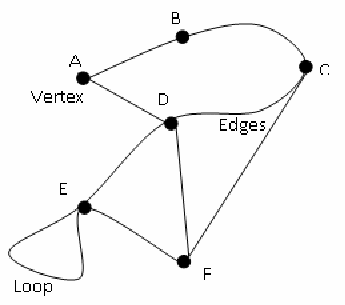
Loop - An edge with the same vertex at each end.
Degree (order) of a vertex - The number of edges meeting at the vertex.
Simple graph - Contains no loops and has no more than one edge between any pair of vertices.
Walk - Sequence of edges. The end of each edge (except the last) is the start of the next.
Trail - A walk with no repeated edges.
Path - A trail in which no vertex is repeated.
Cycle - A closed path. The end of the last edge joins the start of the first.
Hamiltonian Cycle - A cycle that visits every vertex and returns to the start vertex
Hamiltonian Path - A path that visits every vertex.
Connected - There is a path between every pair of vertices in a connected graph.
Tree - Simple connected graph with no cycles.
Digraph (directed graph) - Graph with at least one edge having a direction.
Complete graph - A simple graph with each pair of vertices connected by an edge.
Eulerian Graph &-; A graph in which every path can be traversed exactly once without lifting pen from paper. An Eulerian graph is connected and the degree of every vertex is even.
Incidence Matrix - Matrix representation of a graph. Elements of the matrix show the number of edges connecting the vertices represented by the row and column of the matrix.
Isomorphic - Graphs are isomorphic if one can be deformed to make the other. The vertices can be moved and the edges straightened or bent to do this.
Planar graph - A graph that can be drawn such that no edges cross.
Bipartite graph - A graph joining two sets of objects. Every edge starts in one set and ends in the other.
