Any equation of the form
(1) might be solved using the integrating factor method. This method finds a function of
that the left hand side can be multiplied by so that the left hand side can be written
The integral of this is just
so if we can find a function h(x) we can write the solution down as an integral which may (or may not) be evaluated. The integrating factor for (1) is
Multiplying (1) by
gives
The left hand side can be written
Integrating both sides now gives
Now divide both sides by
to give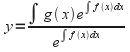
Example: Solve the differential equation
The integrating factor is
Example: Solve the differential equation
The integrating factor is
Dividing by
If the coefficient of
is not 1 it must be made 1.
Example: Solve the differential equation
Divide byto give
The integrating factor is
