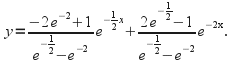Any differential equation of the form
is a second order differential equations and there is a standard technique for solving any equation of this sort. We assume a solution of the form
and substitute this into the equation. We extract the non zero factor – since no exponential is zero for any finite x -
to obtain a quadratic equation. We solve this equation obtain solutions
and
and then the general solution is
and
may be evaluated given suitable boundary conditions, for example
Example: Solve the equation
(1) subject to
and
at
Substitution of the above expressions into (1) gives
We can factor out the nonzeroto obtain
Becauseis non zero we can divide by it to obtain
and we factorise this expression to obtain
and solve to obtain
and
The general solution is then
We now have to find
when
implies
(2)
atimplies
(3)
(2)+(3) gives
then from (2)
The solution is
Example: Solve the equation
(1) subject towhenand
at
Substitution of the above expressions into (1) gives
We can move
to the left hand side and factor out the nonzeroto obtain
Becauseis non zero we can divide by it to obtain
and we factorise this expression to obtain
and solve to obtain
and
The general solution is then
We now have to find
whenimplies
(2)
at
implies
(3)
(2)-(3) gives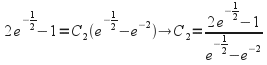
then from (2)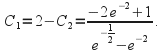
The solution is