The easiest asymptotes to find are those which result from the factorisation of the denominator.
If
then there are asymptotes at
An asymptote that results from the highest power of
in the numerator being one larger than the highest power ofin the denominator or vice versa is also easily found.
- find the equations of the asymptotes.
We divide top and bottom byand take the limit as
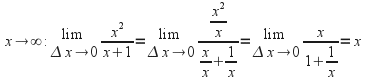
The equation of one asymptote is
and the equation of the other is
since the denominator has a root at
– find the equations of the asymptotes.
we divide top and bottom by
and take the limit as
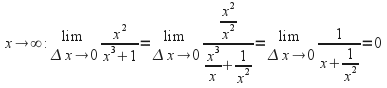
The equation of one asymptote is
and the equation of the other issince the denominator has a root at
If the power ofin the denominator is higher than the power ofin the numerator than there is always an asymptote at
- find the equations of the asymptotes.
We divide top and bottom byand take the limit as
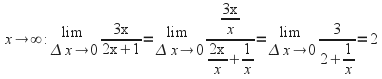
The equation of one asymptote is
and the equation of the other is
since the denominator has a root at
If the highest powers ofin numerator and denominator are the same then there is an asymptote at the quotient of these coefficients.