The sum of a series may not be easily found, and it is desirable to be able to find upper and lower limits for its value. If series consists of terms that are decreasing or decreasing then it may be possible to easily find a bound by integration.
To find the bounds for
note that
is an increasing function. To find a lower bound divide the interval of integration
into
intervals
The minimum value of
on each interval
is
The area of the (k-1)th rectangle is {1 over n}e^{-{n over k}} .
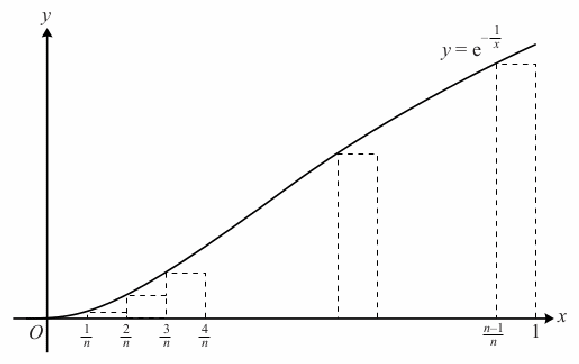
Hence
To find an upper bound for the integral note that the maximum value ofon each intervalis
The area of the
th rectangle,
is
Hence
Hence we can write