An integral domain is a commutative ring with no zero-divisors:
or
Examples
-
The ring
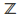is an integral domain. (This explains the name.) -
The polynomial rings
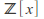and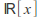
are integral domains.
(Look at the degree of a polynomial to see how to prove this.) -
The ring
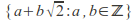is an integral domain. -
If
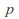is prime, the ring
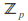is an integral domain.
1 and 3 follow from the properties of real numbers.
2 follows from the linear independence of distinct powers of 
If
and
then
where
If
then the coefficient of
for each
so we have
linearly independent equations each equal 0 and
unknowns (if we treat the
as unknown and solve them in terms of the
) or
unknown (if we treat theas unknown and solve them in terms of the
In either case there are more equations than unknowns so each unknown coefficient is equal to zero.
4 follows from the fact that
or
by Euclid's Lemma hence
or
If
are elements of a field with
then if
it has an inverse
and multiplying both sides by this givesHence there are no zero-divisors and we have that every field is an integral domain.
If
is an integral domain then cancellation for multiplication is permissible. Ifand
then
This follows from thatexists, so