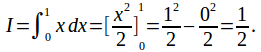Some integrals cannot be calculated exactly. A good example is
The integral exists and is equal to the area A below.
In examples like this it is useful to be able to calculate lower and uppoer bounds for the value of an integral. We can find a lower bound by dividing the interval of integration on the
axis into sunbintervals
and finding the minimum value of the function,
on this interval. Form rectangles with base of length
and heightand area
and add these to get a lower bound for the value of the integral,
To find an upper bound find the maximum value of the function, F-i on each subinterval
Form rectangles of baseand height F-i and area
and add these to get a upper bound for the value of the integral,
To illstrate, find upper and lower bounds for
on
by dividing the intervalinto 5 subintervals
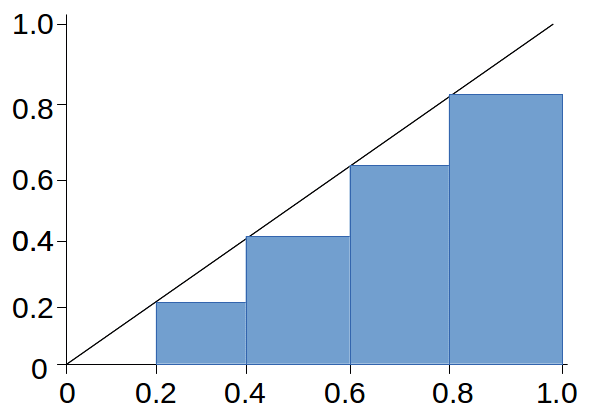
A lower bound is found from the diagram below:
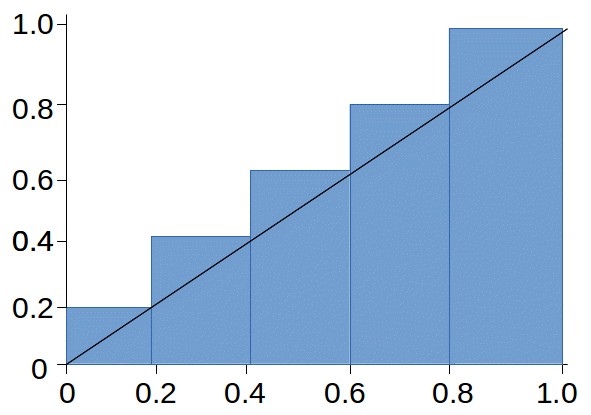
An upper bound for the integral is found from the diagram below.
Compare these bound with the actual value