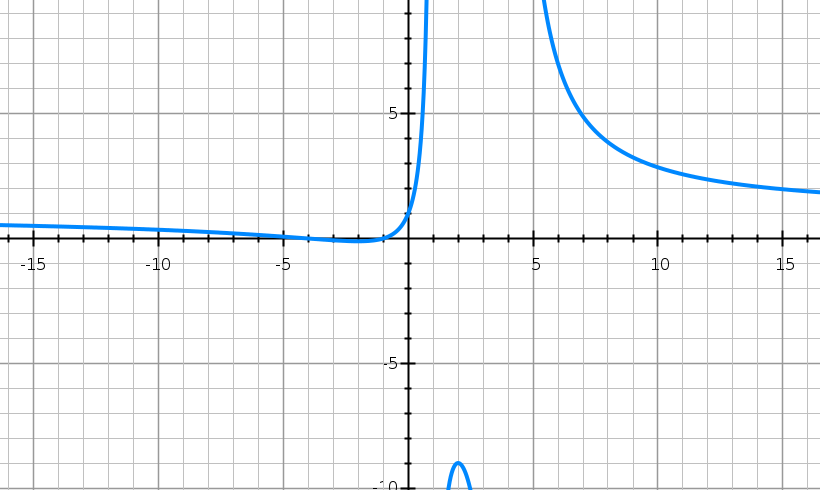
\[y= \frac{x^2+5x+4}{x^2-5x+4}\]
?We can find the turning points by solving
\[\frac{dy}{dx}=0\]
.Differentiating
\[\frac{dy}{dx}= \frac{(x^2-5x+4)(2x-5)}-(x^2+5x+4)(2x+5){(x^2-5x+4)^2}= \frac{-10x^2+40}{(x^2-5x+4)^2}\]
Setting
\[\frac{dy}{dx}=\frac{-10x^2+40}{(x^2-5x+4)^2}\]
implies \[10x^2+40=0 \rightarrow x^2 =4 \rightarrow x = \pm 2\]
.