\[r\]
?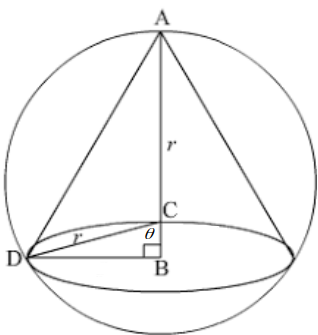
\[rsin \theta\]
and height \[r+r cos \theta\]
.The volume of the cone is
\[V=\frac{\pi}{3} (r sin \theta )^2 \times (r+r cos \theta )=\frac{\pi}{3}r^3sin^2 \theta (1+cos \theta )\]
\[\frac{dV}{d \theta}= \frac{\pi}{3}r^3 (2 sin \theta cos \theta(1+cos \theta)+sin^2 \theta (-sin \theta)=0\]
Hence
\[2sin \theta cos \theta (1+cos \theta)-sin^3 \theta =0\]
.\[sin \theta (2cos \theta (1+cos \theta -sin^2 \theta )=0\]
\[sin \theta (2cos \theta (1+cos \theta -(1-cos^2 \theta )=0\]
\[sin \theta (3cos^2 \theta +2cos \theta -1=0\]
\[sin \theta (3cos \theta -1)(cos \theta +1)=0\]
Hence
\[sin \theta = 0 \rightarrow \theta =0, \; cos \theta = \frac{1}{3}, \; cos \theta =-1 \rightarrow \theta = \pi\]
.Only
\[cos \theta = \frac{1}{3}\]
is possible, then\[\begin{equation} \begin{aligned} V &= \frac{\pi}{3}r^3 sin^2 \theta (1+cos \theta ) \\ &= \frac{\pi}{3}r^3 (1- (\frac{1}{3})^2)(1+ \frac{1}{3}) \\ &= \frac{32 \pi r^3}{81} \end{aligned} \end{equation}\]
