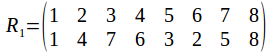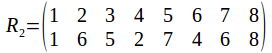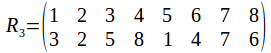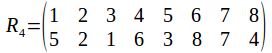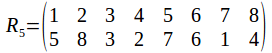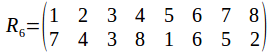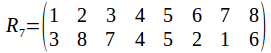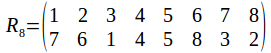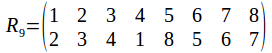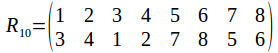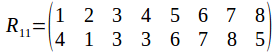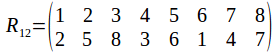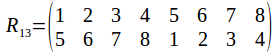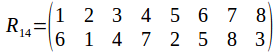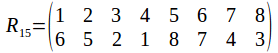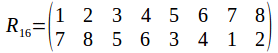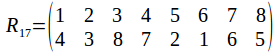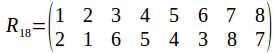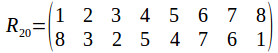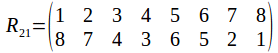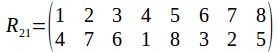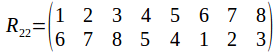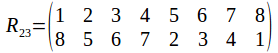The Rotation Group of the Cube

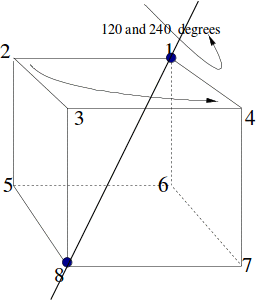
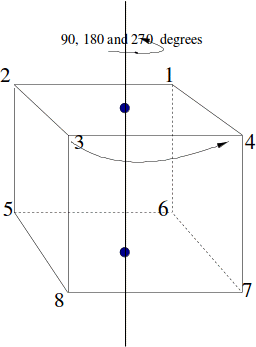
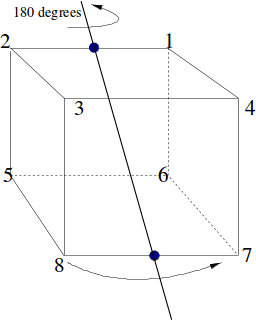
A cube has 12 edges, 8 vertices and six faces. Since any rotational symmetry of the cube must permute the 12 edges, 8 vertices and six sides, you might thing that the group of symmetries of the cube is one of the permutation groupsorIt is non of these, while being a subgroup of all of them. It isTo see why, we can consider the rotational symmetry types of the cube one by one. Label the corners of the cube.

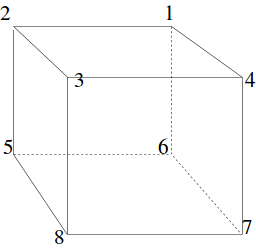
The cube has three axes of rotational symmetry, with rotations of 120 and 240 degrees about each axis.

And of course the rotation group has the identity. Any two identities compose to give a rotation, and the inverse of a rotation is a rotation in the opposite sense. The symmetry group has 24 elements, as doesTo see why it must benot that once a vertex is chosen, the opposite vertices is chosen also, so that while there are 8 vertices, there are only four pairs of vertices. Each pair of vertices can be labelled  1, 2, 3 or 4. Any pair of vertices can transformed onto any other while transforming the other pairs or fixing them, so the complete set of labels is used.