![]() is continuous and bounded on
is continuous and bounded on![]() so it seems that it should be Riemann integrable. It behaves very strangely though as
so it seems that it should be Riemann integrable. It behaves very strangely though as![]() as shown below.
as shown below.
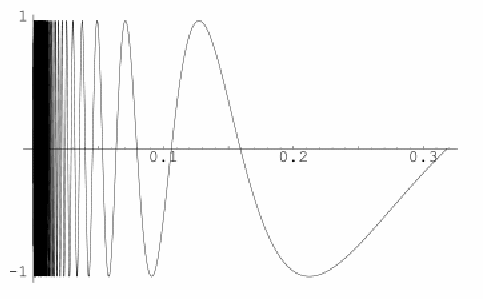
As![]() gets closer and closer to
gets closer and closer to![]() takes on all values in
takes on all values in![]() and since
and since![]() is
is![]() periodic it takes the same value whenever
periodic it takes the same value whenever![]() increases by
increases by![]() As
As![]() this happens an infinite number of times.
this happens an infinite number of times.
![]() can be shown to be Riemann integrable by splitting
can be shown to be Riemann integrable by splitting![]() into two intervals
into two intervals![]() and
and![]() Over the first interval
Over the first interval![]() and
and![]() so the integral of
so the integral of![]() over this region is
over this region is
![]()
![]()
Over the second integral there are no problems because![]() is continuous and bounded so is Riemann integrable over this interval. Then
is continuous and bounded so is Riemann integrable over this interval. Then![]() where
where![]() is taken over the interval
is taken over the interval![]() and since
and since![]() is Riemann integrable over this period,
is Riemann integrable over this period,![]() Let
Let ![]() then
then![]() and
and![]() is Riemann integrable on
is Riemann integrable on![]()
