These inequalities state the pretty obvious fact that you don't have to travel as far if you go direct.
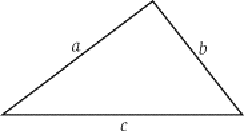
For the triangle above we may write
Proof: As a vector we may write
hence
and
The expression on the right hand side factorises into a perfect square:
Now square root both sides to obtain
It is important to realise that
and
can in general be vectors or numbers. This expression is called the 'forwards' form of the triangle inequality. There is also a 'backwards' form:
The backwards form is quite easy to prove by considering the two cases
and
separately.
In either caseis satisfied.