A function
is Riemann integrable if it is continuous and bounded on a closed interval. Of course, if a function is differentiable then it is continuous and hence Riemann integrable but there are many examples of functions which are bounded but not continuous on a closed interval but which are still Riemann integrable.
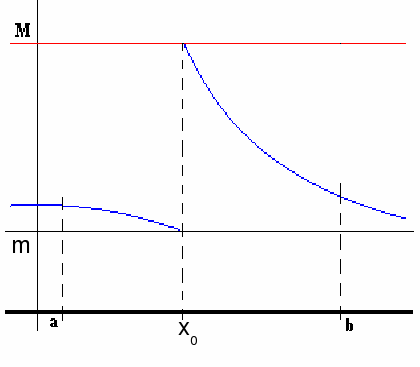
A simple example is shown above. The function has a discontinuity at
but is still Riemann integrable because this discontinuity occupies an interval of length zero. In fact if we construct a partition consisting of subpartitions on
thenis Riemann integrable on
and
since it is bounded and continuous on these subintervals and on the subinterval
we have
and
so
(1)
Let
then
so Riemann integrability amounts to being Riemann integrable on the intervals
This can be extended, so that a function with a finite numbers of discontinuities, each of length zero, is Riemann integrable. Another example is given by the function