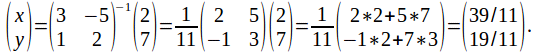The simultanous equations
x+2y=5
x-y=2
has the unique solution x=3, y=1.
We can write the system in matrix form as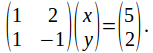
Then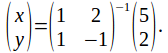
The condition nexcessary for a unique solution to exist is then that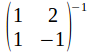 exists, OR, since
exists, OR, since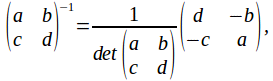 that
that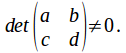
We can generalize this.
If a system of linear equations can be associated with a square coeefficient matrix with non zero determinant, then the system has a unique solution. More specifically, if we can write a system of linear equations in the form![]() where
where![]() is a square matrix and
is a square matrix and![]() is the vector of variables to be solved for, then
is the vector of variables to be solved for, then![]()
Example: Find if the system of equations
![]()
![]()
![]()
has a unique solution, and if so find it.
The third equation is reduncant, since it is twice the second equation. The system is equivalent to the system
![]()
![]()
The coeefficient matrix is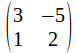 with determinant
with determinant![]() so the system has a unique solution, given by
so the system has a unique solution, given by