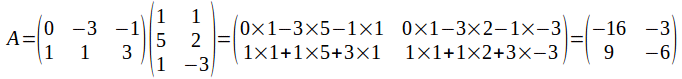It is not always the case that matrices can be multpiled. Matrices A and B can only be multipled if rows and columns match up so that if we are to find the product AB, the number of columns of A is equal to the number of rows of B.
More concisely, we can say a matrix is an r by c matrix if it has r rows and c columns.
If matrix A is an m by n matrix and matrix B is an p by q matrix then AB exists if and only n=p. The product AB is an m by q matrix.
Example: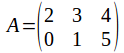 and
and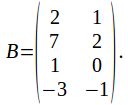
A is a 2 by 3 matrix and B is a 4 by 2 matrix. Since 3 neq 4 the product AB does not exist.
Example: and
and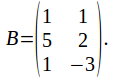
A is a 2 by 3 matrix and B is a 3 by 2 matrix. Since 3 =3 the product AB exists and will be a 2 by 2 matrix.