An improper integral is one where either of the following holds
one of the integrals is
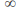 or
or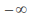 or the limits are
or the limits are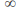 and
and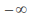
![]() and
and![]() are all improper integrals.
are all improper integrals.
the integrand (the function being integrated) includes a term evaluated at one or both limits which takes the form
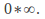
![]() and
and![]() are all improper integrals. The first of these integrands,
are all improper integrals. The first of these integrands,![]() includes the factor
includes the factor![]() which tends to
which tends to![]() as
as![]() tends to
tends to![]() and
and![]() which tends to 0 as
which tends to 0 as![]() tends to infinity . The second includes the factors
tends to infinity . The second includes the factors![]() and
and![]() which tend to
which tend to![]() and 0 respectively as
and 0 respectively as![]() tends to
tends to![]() The third includes the terms
The third includes the terms![]() and
and![]() which tend to 0 and
which tend to 0 and![]() as
as![]() tends to 0.
tends to 0.
Improper integrands can often be evaluated because the integrand tends to 0 at the troublesome limit, or if the integrand is of the form![]() at one or both limits, one factor tends to 0 faster than the other tends to infinity. This is true for the improper integral
at one or both limits, one factor tends to 0 faster than the other tends to infinity. This is true for the improper integral![]() tends to zero faster than any power of
tends to zero faster than any power of![]() tends to infinity,
tends to infinity,![]() so we may write
so we may write
![]()
Having the integrand tend to zero at the limits is not sufficient for the integral to be able to be evaluated. The integrand must tend to 0 fast enough. The integral![]() is not defined because
is not defined because![]() does not tend to 0 fast enough. In fact,
does not tend to 0 fast enough. In fact,![]()
