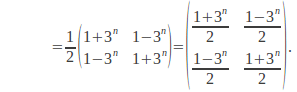Given a matrix
with non zero entries only on the leading diagonal, it is very easy to find powers of
If for example,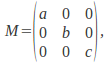
then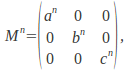
A matrix
is said to be diagonalizable if we can find a matrix
such that
or equivalently
where
is a diagonal matrix with non zero entries only on the leading diagonal. Of course only square matrices can be diagonalized, but a wide range of square matrices can be diagonalized. If a matrix is diagonalizable, then
since when the brackets are removed each occurrence of
reduces to the identity matrix.
The matrixexists in the case when the
timesmatrixhasindependent eigenvectors. The eigenvectors form a linearly independent set, so a matrixwhose columns consist of them can be inverted thenfound using
Example: The matrix
has eigenvalues 1 and 3 with eigenvectors
and
so that
and
D is the matrix with diagonal entries equal to the eigenvalues, with the eigenvalues in the column of that corresponding eigenvector:
is then given by
