A probability distribution tells you the probability of something happening,
the probability of the random variable
taking the value
A Cumulative distribution tells you the probability of the random variabletaking a value less than or equal to a value
often written
Given a probability distribution
we can find the cumulative distribution:
Ifis presented in a table, add the entries as you go along.
|
|
1 |
2 |
3 |
4 |
5 |
|
|
0.1 |
0.3 |
0.15 |
0.05 |
0.4 |
|
|
0.1 |
0.1+0.3=0.4 |
0.1+0.3+0.15=0.55 |
0.1+0.3+0.15+0.05=0.6 |
0.1+0.3+0.15+0.05+0.4=1 |
Ifis presented as a function, integrate. Suppose
then
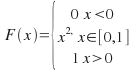
Given a cumulative distribution
we can find the probability distribution:
Ifis presented in a table, subtract successive entries as you go along.
|
|
1 |
2 |
3 |
4 |
5 |
|
|
0.1 |
0.4 |
0.55 |
0.6 |
1 |
|
|
0.1 |
0.4-0.1=0.3 |
0.55-0.4=0.15 |
0.6-0.55=0.05 |
1-0.6=0.4 |
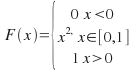Ifis presented as a function, differentiate. Supposethen
