If two quantities are related, there will probably be a correlation between them. An increase in one may cause an increase in the other, so that the two quantities are positively correlated, or an increase in one may cause a decrease in the other, so that the two quantities are negatively correlated. However, two quantities may still be in a perfect correlation with no such relationship between them. The diagram below shows a near perfect relation between the speed of water flow in a river and distance from the river bank, but the correlation coefficient is zero.
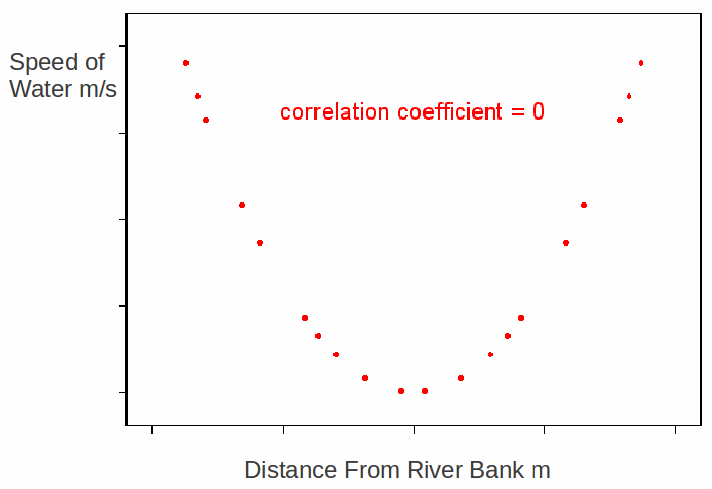
This is because the correlation coefficient only measures goodness of fit to a straight line.
In addition a near perfect relationship may exist between quantities that have no influence on each other. The is a very good relationship between accumulated rainfall and the sum of all the money ever spent on chocolate bars – both inevitably increase, but an increase in one does not cause the other to increase. Even if such a relationship exists for good reason, it may be impossible to identify which variable causes the other to change. One example is obesity and heart disease. Arguments can be made for each to cause the other, and it is impossible to identify which is the cause and which the effect, and therefore which is the independent variable and which is the dependent. By convention, the independent variable is plotted on the
– axis, and the dependent variable on the
– axis.