Composing Functions
Some functions can be extremely complicated, for example,
It is often simpler to represent a single function as two separate functions, one carried out on the result of the first. For example, we are given the function
(1)
We could define the two functions
and
and then
To find
we could use (1):
Or we could find
then
then
Example
Find
and
Inverses of Functions
There is a simple procedure for finding the inverse of a function
which is equivalent to reflecting the graph of
in the line y=x
-
Given
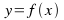make x the subject. -
Swap all the x's and y's over so now there is only one y which is the subject of the equation.
-
Replace the single y with
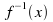
Example:
Find
Example
