Differentiating Between Unbiased Estimators

When choosing an estimatorfor a statisitical parameter we are primarily interested insimplicity of calculation and the bias of the estimator.

The bias of a statisiticalparameter is the difference between the estimator for the parameterand the true value of the parameter. If the estimator for apopulation parameteristhen

We are usually interested inselecting the estimator with the smallest bias, since it will becloser to the actual value of the population parameter more often onaverage that any other estimator.

Suppose we are interested infinding an estimator for the population mean,Wehave a choice of estimators:

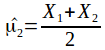whereandareindividual measurements from the population

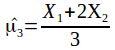whereandareindividual measurements from the population

Each of these estimators isunbiased, since

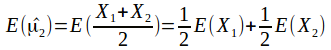
If the variance ofisthenthe variance ofis

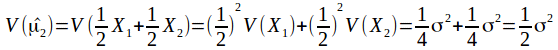
and the variance ofis

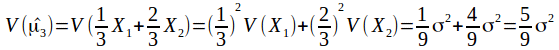
Of all these estimatorsforhasthe smaller variance, soisthe best estimator.