The Geometric Distribution

The geometric distribution models players of a game 'in search ofsuccess' . When a player wins they stop playing. There are threeconditions the game must satisfy:

1. When the player wins he stops playing, or at least thegeometric distribution ceases to model the game at this point. Ifthe player continues to play, a new geometric distribution isrequired.

2. The probability of winning each game is a constant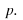Ifthe players get better as more games are played then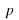isnot constant and the distribution cannot be geometric.

3. Each game is independent. If a player loses he is not morelikely to win the next time and vice versa.

If the probability of winning isandthe player wins – and stops playing – at the n^th attemptthen the player must havefailuresbefore this success. Since each failure is independent withprobability theprobability of this isandsince they win on the next attempt with probabilitywe havethisis called the probability mass function – discrete distributionshave probability mass functions as opposed to the probability densityfunctions for continuous distributions.

The expected number of attempts to win the game is

We can also find the variance:

Then

and

This is called the cumulative mass function.