The fundamental equation connecting capacitance, voltage and charge is![]()
Charge=Voltage*Capacitance (1)
If a battery is connected to a capacitor, the voltage across the capacitor will not instantly become the battery voltage. Instead current will flow in the circuit. Negative charge will collect on one plate and positive charge on the other. The voltage across the capacitor will build up and as it does the voltage available to drive the current through the internal resistance of the battery will decrease. Eventually after an infinite time, the voltage across the capacitor will reach the battery voltage and no current will flow. At each point during the charging of the capacitor equation (1) is obeyed. We can also related the voltage across the capacitor to the time elapsed since the battery was connected:![]() where
where![]() is the emf of the battery.
is the emf of the battery.
But then (1) gives the charge across the capacitor at any time![]() since if we multiply both sides by
since if we multiply both sides by![]() we obtain
we obtain![]() where
where![]() is the charge stored on the fully charged capacitor.
is the charge stored on the fully charged capacitor.
We can also find the current in the circuit at any time![]() by differentiating
by differentiating![]() obtaining
obtaining![]() (2)
(2)
Now![]() Substituting this into (2) gives
Substituting this into (2) gives![]()
But![]() is the initial current
is the initial current![]() so
so ![]() The qualitative graphs of
The qualitative graphs of![]() and
and![]() are shown below.
are shown below.

Similar arguments give the analogous equations for discharging capacitors.
![]() and
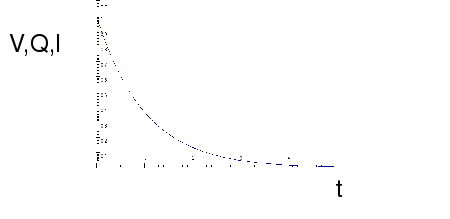
and![]() The qualitative graph of V,Q and I against t is shown below, indicating exponential decay.
The qualitative graph of V,Q and I against t is shown below, indicating exponential decay.