\[\mathbf{F}= \mathbf{E} q + q \mathbf{v} \times \mathbf{B}\]
, the net force on a particle can be made zero if the electric and magnetic forces cancel.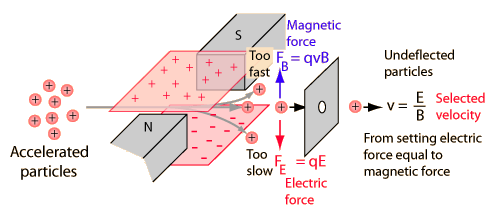
\[B=\frac{E}{v}\]
.In this equation the mass of the charged particle does not appear and it might seem that the mass of the particle does not matter. This is not always true. Suppose for example that the particle of mass
\[m\]
is accelerated through a potential difference \[V\]
. The particle loses electrical potential energy \[qV\]
and acquires kinetic energy \[\frac{1}{2}mv^2\]
.Equating these gives
\[qV=\frac{1}{2}mv^2 \rightarrow v= \sqrt{\frac{2qV}{m}}\]
.The speed acquired by the particle decreases with increases
\[m\]
.For this particle entering an electric field of strength
\[\mathbf{E}\]
the force is \[\mathbf{F}= q \mathbf{E} + q \sqrt{\frac{2qV}{m}} \mathbf{e}_v \times \mathbf{B} \]
.The force is clearly mass dependent and the forces cannot cancel for charges of different mass accelerated through the same potential difference.
