\[C\]
in series with a resistor of resistance \[R\]
and an EMF of voltage \[V\]
as it discharges is\[Q(t)=Q(0)e^{- \frac{t}{RC}}\]
and the voltage across the capacitor is
\[V(t)=V(0)e^{- \frac{t}{RC}}\]
The energy stored in the capacitor is
\[E(t)=\frac{1}{2} Q(t)V(t)=\frac{1}{2}Q(0)e^{- \frac{t}{RC}} V(0)e^{- \frac{t}= \frac{1}{2}Q(0)V(0)e^{- \frac{2t}{RC}}{RC}}\]
The fraction of charge left on the capacitor after a time
\[t\]
is\[\frac{Q(t)}{Q(0)}=e^{- \frac{t}{RC}}\]
The fraction of the original voltage on the capacitor after a time
\[t\]
is\[\frac{Q(t)}{Q(0)}=e^{- \frac{t}{RC}}\]
The fraction of the original energy stored in the capacitor after a time
\[t\]
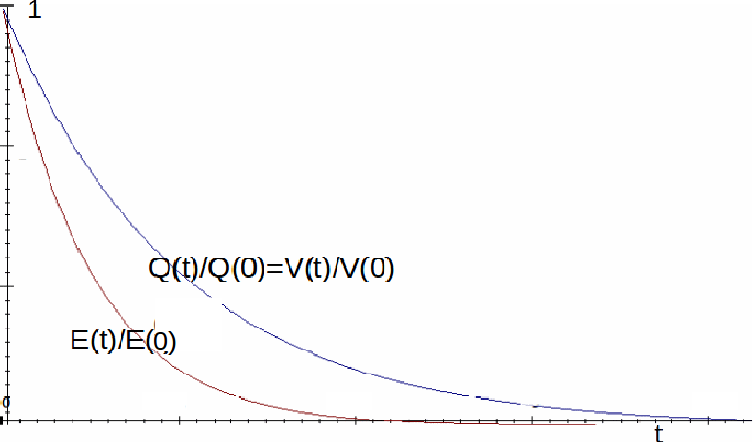
is\[\frac{E(t)}{E(0)}=e^{- \frac{2t}{RC}}\]
The factor
\[\frac{E(t)}{E(0)}=e^{- \frac{2t}{RC}}\]
decreases as
\[(e^{- \frac{t}{RC}})^2 =(\frac{Q(t)}{Q(0)})^2 = (\frac{V(t)}{V(0)})^2\]
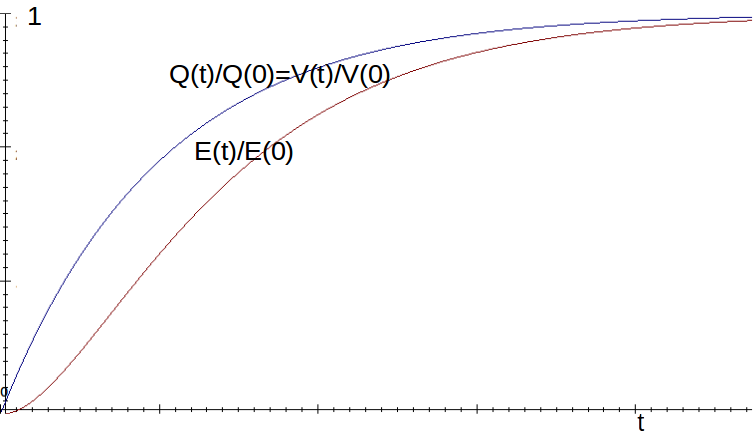
The energy stored in the capacitor decreases much fast than either the charge or the voltage as it discharges. As the charge on the capacitor halves, the voltages halves but the energy decreases by three quarters. Conversely, the energy stored in the capacitor increases much slower than either the charge or the voltage as it charges. As the charge increases to half of its final value, the voltage increases to half of its final value but the energty increases to one quarter of its final value.
Charging Capacitor
DisCcharging Capacitor