Impedance and Inductance and Capacitor and Resistor in Series

The Inductance of a capacitor or inductor depends on the geometrical properties of the capacitor or inductor.

We would expect the inductance – or resistance of an inductor to ac current - of an inductor to increase with the frequency because rapid changes of voltage and polarity induce large back EMF's and the inductance -or resistance of a capacitor to ac current – to decrease with frequency because if the frequency increases there will not be enough time to build up large charges or (back) voltages across the the capacitor.

In fact the inductance of an inductor is given by

And the Inductance of a Capacitor is given by

Hence in a purely Capacitative circuit we can write

And in a purely inductive circuit we can write

Things become a great deal more complicated when we have resistances, inductors and capacitors all in the same circuit. If these components are in series, we cannot just add the inductances as we could with resistances in series. The problem is that the resistances of the capacitor and inductor ore “opposed”, ie it is possible, when you have inductors and capacitors in the same circuit, for one of the components to have negative resistance. On the other hand, a resistance is always a normal, common sense resistance. This is illustrated below:

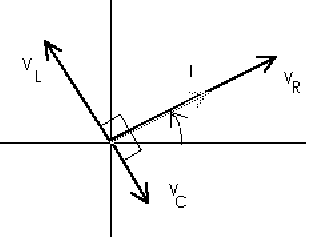
The Voltagehas the same phase as I but the Voltage across the Inductorleads the current byand the voltage across the inductor lags the current byThe net voltage in thedirection isWe can find the resultant of all three components of Voltage as illustrated below.

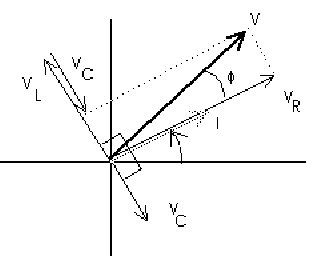
or, since V = I Z, we can now write the total impedance Z for this series RCL circuit as

Whenthe inductance and effective resistance of the circuit is a minimum. The circuit is said to be “matched” or in resonance. We have,or