Apparatus:
2 x metre rulers, knife-edge, set of 100g masses, vernier callipers, micrometer
Diagram:
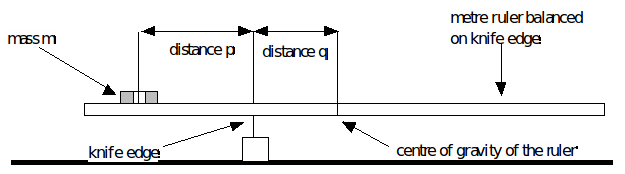
Procedure:
1. Place the one of your metre rulers (without the mass, m shown in the above diagram) on the knife-edge so that it is balanced. The knife-edge should be roughly below the 50cm mark on the ruler. Note down the precise position of the knife-edge below the ruler to the nearest mm. This is the position of the ruler's centre of gravity.
2. Place a 100g mass near the left-hand end of the ruler as shown in the diagram above. The ruler will tip down on this side.
3. Move the knife-edge towards the mass until the ruler again balances.
Measure the distance p (in mm) between the centre of the mass and the new knife-edge position and the distance q (in mm) between the new knife-edge position and the position of the centre of gravity of the ruler (see diagram above).
4. Repeat stages 2 & 3 for a masses, m of 200g to 600g.
5. Measure as accurately as possible the volume, V of the metre ruler you have been using.
6. When the ruler is balanced the anticlockwise moment caused by the weight of the masses is equal to the clockwise moment caused by the weight of the ruler. Therefore weight of mass, m x distance p = ruler weight x distance q
7. Draw a graph of distance p against q ÷ m
8. Measure the gradient of this graph.
The gradient is equal to the mass of the ruler, M.
9. Calculate the density of the ruler, density = M / V.
11. Answer the following:
(a) Explain why the gradient of your graph is equal to mass of the ruler.
(b) Estimate the % uncertainty in:
(i) the mass measurement
(ii) the volume measurement
(iii) the density calculation.
