Apparatus:
500ml beaker, crushed ice, 0 – 100 C thermometer, thermistor in a balloon, retort stand, clamp, boss and a digital multimeter.
Introduction:
You are probably aware that the resistance of a thermistor varies temperature as shown in the sketch graph below.
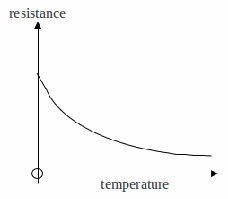
Two, students A and B make the following different statements about this relationship.
Student A suggests that the resistance is inversely proportional to the temperature.
Student B suggests that relationship is like that of exponential decay, that is that the resistance decreases with temperature in the same way that the activity of a radioisotope falls over time.
Procedure:
1. Explain how you can tell, from the sketch graph alone, that student A's statement is incorrect.
2. You are now going to try to test student B's statement.
3. Using the digital multimeter, find how the resistance of your thermistor (
) varies with temperature (
/ C).
The thermistor is in a balloon which in turn is to be placed in a beaker of water over a bunsen.
Start with a beaker full of ice and so obtain a resistance reading at a temperature of about 0 C.
4. Remove all of the ice and then note resistance readings for temperatures between about 20 C and about 100 C. The thermistor is in a balloon as direct contact with water would cause problems because water is a conductor of electricity. This does however mean that it takes time for the inside of the balloon to reach the temperature of the water so adopt the following procedure between readings:
Heat the water and when the thermometer reading is within about 3 degrees of the required temperature, remove the bunsen flame and allow the temperature to steady making sure that the water is well stirred. Then take the resistance reading and go on to the next temperature.
5. Calculate the kelvin temperature for each of your temperatures where:
kelvin temperature (K) = C + 273
Insert your readings into a four column table with headings the bold parts of:
temperature in C
kelvin temperature; (T / K);
resistance ()and natural logarithm of resistance
6. Plot a graph of
against temperature in kelvin
7. If student B is correct the graph should form a straight line of negative gradient.
8. Comment on how well, or otherwise, your graph backs up student B's statement.
9. Explain the mathematics behind the statement in stage 7.