If you measure the voltage across the terminals of a battery (below left), then connect the battery to a resistor and measure the voltage across the resistor (below right) it is never quite equal to the voltage you first measured across the terminals of the battery.
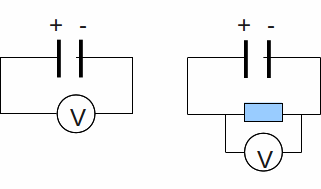
Some of the voltage battery is missing – the 'missing volts'. The reason is that the battery itself has some resistance, and some of the battery voltage – the emf or electromotive force, actually the energy per unit charge supplied by the battery – must be used to drive the current through the battery.
Alternatively we may say that the power made available to the external circuit – the resistor – is less than the power supplied by the chemical reaction inside the battery, with the difference being that power needed to drive the current against the internal resistance of the battery.
There is an equation to model the situation. If the emf of the battery is E and a current I flows through the resistance R, then the voltage across this resistance is IR and the lost volts is
For the circuit above right, the current through the batter is
so if the internal resistance of the battery is
the lost volts is
and we can write
(1)
We can find the emf
of a battery and it's internal resistance
using the circuit below.
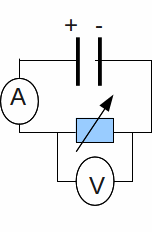
By varying the resistance, we can vary the voltage and current. Write (1) as
where 
the voltage across the variable resistor. Then
which is of the form
Values of
against
can be plotted. The gradient of the graph is
and the intercept is