It is linear. If we have two charge distributions and bring them together the total force is the vector sum of the forces due to the two charge distributions.
The force on a charge
\[Q\]
at point A due to a point charge \[q_B\]
at a point B is \[\mathbf{F}_{BA}=\frac{1}{4 \pi \epsilon_0} \frac{q_B Q}{r^2_{AB}} \mathbf{e}_{BA}\]
where \[r_{AB}\]
is the distance from A to B, \[\epsilon_0 = 8.854 \times 10^{-12} F/m\]
and \[\mathbf{e}_{BA}\]
is the unit vector from B to A.Suppose then that we have five charges as shown.
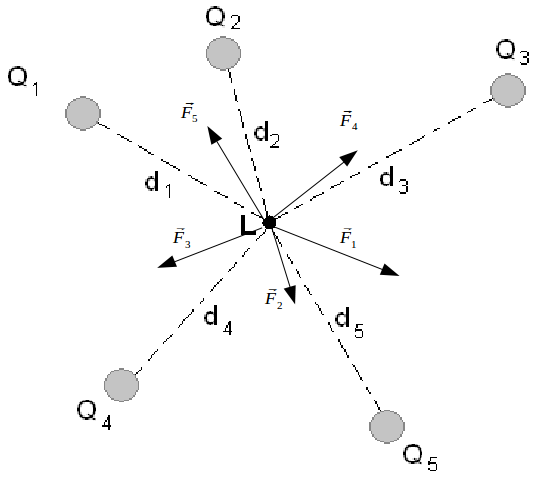
Each gives rise to a force, but the overall force is
\[\begin{equation} \begin{aligned} \mathbf{F} &= \mathbf{F}_1+\mathbf{F}_2+\mathbf{F}_3+\mathbf{F}_4+\mathbf{F}_5 \\ &= \frac{1}{4 \pi \epsilon_0} \frac{q_1Q}{d^2_1}\mathbf{e}_{1A}+ \frac{1}{4 \pi \epsilon_0} \frac{q_2Q}{d^2_2}\mathbf{e}_{2A}+ \frac{1}{4 \pi \epsilon_0} \frac{q_3Q}{d^2_3}\mathbf{e}_{3A} + \frac{1}{4 \pi \epsilon_0} \frac{q_4Q}{d^2_4}\mathbf{e}_{4A} + \frac{1}{4 \pi \epsilon_0} \frac{q_5Q}{d^2_5}\mathbf{e}_{5A} \\ &= \frac{Q}{4 \pi \epsilon_0} (\frac{q_1}{d^2_1}\mathbf{e}_{1A} + \frac{q_2}{d^2_2}\mathbf{e}_{2A} + \frac{q_3}{d^2_3}\mathbf{e}_{3A} + \frac{q_4}{d^2_4} \mathbf{e}_{4A} + \frac{q_5}{d^2_5} \mathbf{e}_{5A}) \end{aligned} \end{equation} \]
