The best way of representing how the electric potential varies around a charged object is to identify the regions where the potential is the same. These are called equipotential surfaces. They are closed surfaces in three dimensions but we can often represent them in two dimensions as curves. The diagram below shows curves on the equipotential surface – in reality the charge is in a three dimensional space and the equipotential surfaces are concentric spheres.
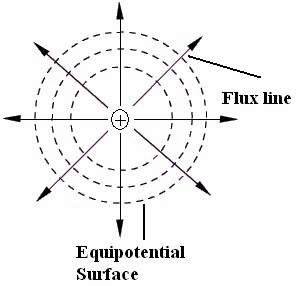
Notice that the flux or field lines are at right angle to the equipotential surfaces wherever they meet. This is in fact true in general for equipotentials and flux lines, a consequence of the fact that the force on a particle acts in the direction of the greatest rate of change of potential, which is always perpendicular to the equipotential. The flux lines of course, indicate the direction of the electric field, and the direction of the force on a positive charge.
The closer together the equipotentials, the stronger the electric field, since the gradient (and force) is most rapid where the equipotentials are closest. For this reason, the relative strength of an electric field at different points can be estimated by considering the equipotentials.
Equipotentials are always closed surfaces around a distribution of charge, though they may take different forms at different distances from the charges, while always smoothly deforming. The surface of a conductor is always an equipotential, since charge is free to move on the surface so as to equalise the potential everywhere. The surface being an equipotential, the electrical field is always perpendicular to the surface.