\[V\]
. This potential field has some a special property.It is linear. If we have two charge distributions and bring them together the potential at each point is the sum of the two individual potentials.
The potential at a point A due to a point charge
\[q\]
at a point B is \[V=\frac{1}{4 \pi \epsilon_0} \frac{q}{r_{AB}}\]
where \[r_{AB}\]
is the distance from A to B and \[\epsilon_0 = 8.854 \times 10^{-12} F/m\]
.Suppose then that we have five charges as shown.
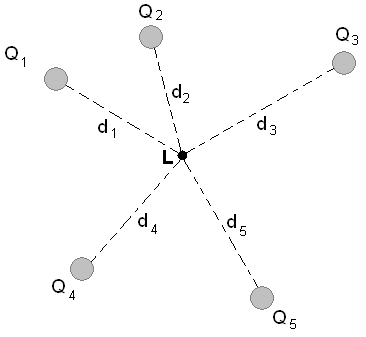
\[\begin{equation} \begin{aligned} V &= V_1+V_2+V_3+V_4+V_5 \\ &= \frac{1}{4 \pi \epsilon_0} \frac{q_1}{d_1}+ \frac{1}{4 \pi \epsilon_0} \frac{q_2}{d_2}+ \frac{1}{4 \pi \epsilon_0} \frac{q_3}{d_3} + \frac{1}{4 \pi \epsilon_0} \frac{q_4}{d_4} + \frac{1}{4 \pi \epsilon_0} \frac{q_5}{d_5} \\ &= \frac{1}{4 \pi \epsilon_0} (\frac{q_1}{d_1} + \frac{q_2}{d_2} + \frac{q_3}{d_3} + \frac{q_4}{d_4} + \frac{q_5}{d_5}) \end{aligned} \end{equation} \]
