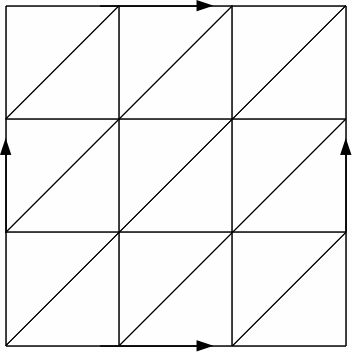
Triangulation is the division of a surface or plane polygon into a set of triangles, with the condition that each side of each triangle side is entirely shared by two adjacent triangles. Every surface has a triangulation, maybe with an infinite number of triangles. A surface with a finite number of triangles in its triangulation is compact.
Thr triangles do not have to be straight lines. This is because we need to be able to triangulate curved surfaces, on which every edge is a curve, and angles may not add to 180 degrees. The condition for a subdivision of a surface to be a triangulation are as follows:
Every face (triangle) has three edges and three vertices. This implies that each face is homeomorphic to a disc.
Every edge has two vertices.
There is at most one fact with three given vertices.
There is at most one edge with two given vertices.
The subdivision below lef is not a triangulation of the torus because after identification of the opposite sides, there is only one vertex.
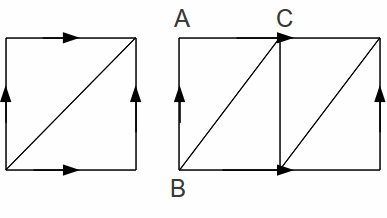
Neither does the subdivision above right, because the edge AB has only one vertex, after identifications. Nor does the triangle ABC have three distinct vertices. The subdivision below has two triangles, A and B with the same vertices, after identification.
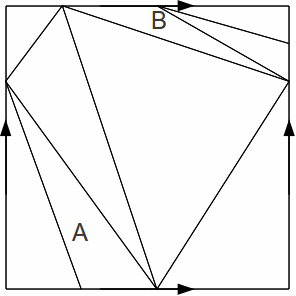
The subdivision below is a possible triangulation.