The Smallest Topology Containing Subsets of a Set

Proof

Letbe a set and letbe a family of subsets ofso thatthe discrete topology. There is a unique smallest topologysuch thatgiven by

is said to be generated by A.

Proof

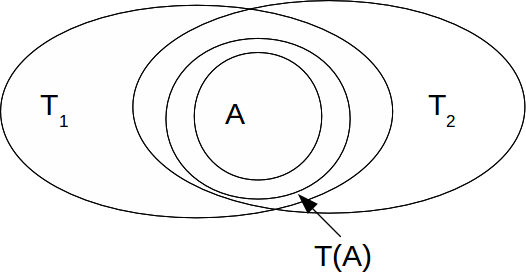
Letand letbe the intersection of all topologiescontaining

is a topology since

1.for eachso

2. Iffor eachthenfor eachso

2. Iffor eachthenfor eachso

Sinceis the intersection of all the topologies containingit must be the smallest topology containingIf there is any other smallest topologythenis a smaller topology than eitherorcontaining A - a contradiction - sois unique.

Also sinceandis a topology, it must contain all intersections and unions of elements of