The Six Colour Theorem states:
Any regular map (so that all the vertices have the same order) on a surface of Euler characteristic greater than zero requires at most six colours if neighbouring colours are coloured differently.
Obviously the six colour theorem is true for a map with six or less faces or countries F<=6. A map must contain at least one face with less than 6 edges. Suppose we shrink this face to a point. The possibilities are shown below.
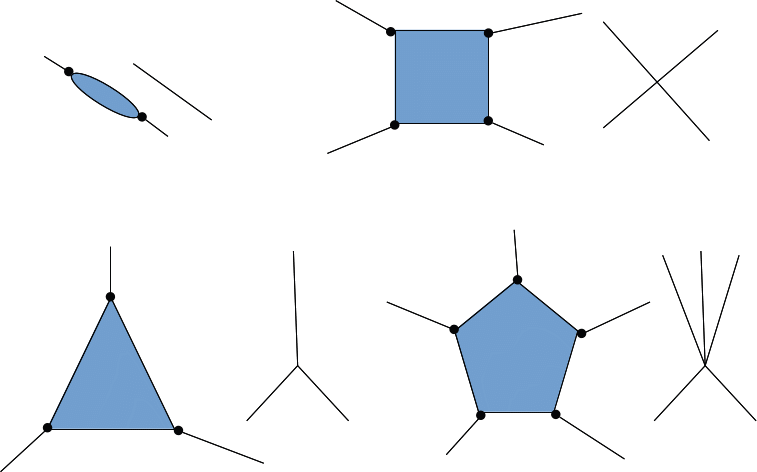
For ech of these contracted maps, the theorem holds by assumption so each of the contracted maps can be coloured by at most six colours. When the face is restored there is a colour available (since the face is bordered by at most six other faces). Hence, if the theorem is true for F faces, it is also true for F+1 faces.
