The gradient of a graph often represents an important physical quantity. The gradient of a distance time graph is the velocity, and the gradient of a graph of potential energy against distance is the negative of the force acting on a body. Actually, to be completely accurate, the gradient at a point on a distance time graph is the velocity at that time (the time will be read off the horizontal axis), and the force on a body is the negative gradient of the potential energy plotted against distance at a point.
To find the gradient of a graph at a point draw a tangent to the graph and construct a right angled triangle with the base parallel to the horizontal axis and the height parallel to the vertical axis.
The gradient will then be the height dividing by the base, with the proviso that the gradient is positive if the graph is going up from left to right and negative if the graph is going down from left to right.
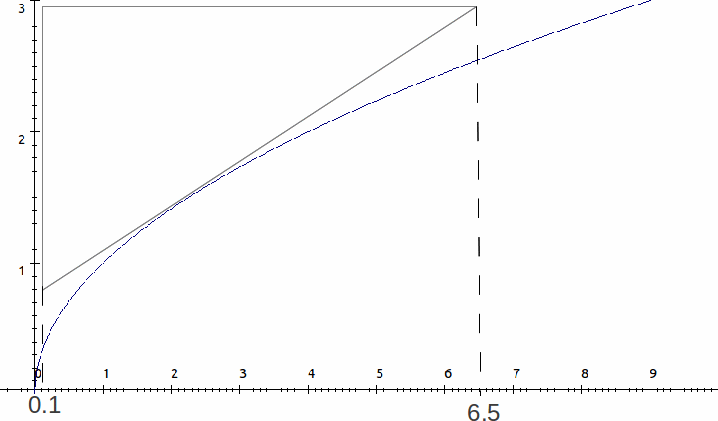
The height of the triangle above is about 3 -0.8=2.2 and the base is about 6.5-0.1 =6.4 so the gradient is
(positive since the graph is going up from left to right).