The simple pendulum executes approximate simple harmonic motion. A pendulum is illustrated below. At the point P all the forces acting on the pendulum are shown. The path of the pendulum is an arc of a circle since the string is inextensible.
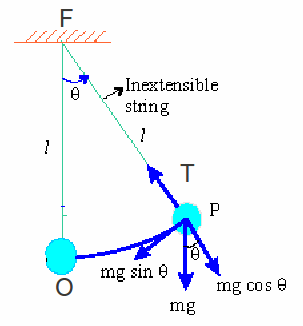
Resolving at P for the pendulum:
Towards F:
(1)
Applying
along the tangent of the arc PO:
(2)
The minus sign indicates the acceleration is in the direction of decreasing
Equation (1) we can ignore since the motion is along the arc of the circle and this equation is derived by resolving perpendicular to the motion.
We consider equation (2). If
is small then
(2) becomes
The length of a circular arc is
and the acceleration of the pendulum above is
(3)
If we make the substitution
then the above equation (3) becomes
which has the form of the simple harmonic motion equation.