Simple differential equations take the form
We have to solve the equation to find
as a function of
We do this by putting all the
's on the right and integrating. Normally when we integrate we have to add a constant. We can find the value of this constant if we are told a point on the curve.
For example, dy over
The point
lies on the curve. Findas a function of
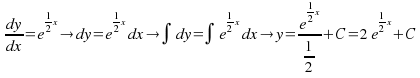
We now have to find C. We are told in the question that y=0 when x=5. Hence
Example:
The point
lies on the curve. Find y as a function of x.
We now have to find C. We are told in the question that
when
Hence
Example
The point
lies on the curve. Findas a function of
We now have to find C. We are told in the question that
when
Hence
