\[y=f(x)\]
, we can find \[\frac{dy}{dx}\]
and solve \[\frac{dy}{dx}=0\]
. This will give us some values of \[x\]
. Substituting these values into the expression \[y=f(x)\]
will give us the \[y\]
and allow us to write down the points \[(x,y)\]
.To find if the point is a maximum or minimum we differentiate again to find
\[\frac{d^2y}{dx^2}\]
, and substitute the relevant \[x\]
. If the result is positive, the point is a minimum. If the result is negative, the result is a maximum.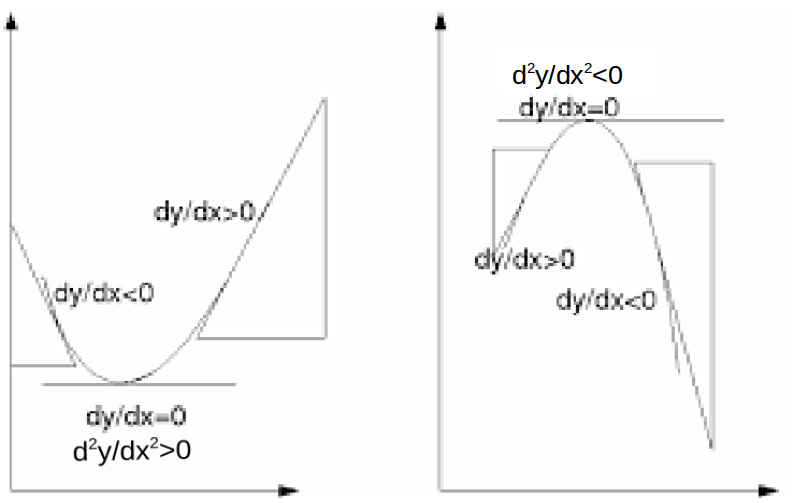
\[y+x^2-8x+2\]
and determine the type of point.\[\frac{dy}{dx}=2x-8\]
We solve
\[\frac{dy}{dx}=2x-8=0 \rightarrow x=4\]
.Then
\[y=x^2-8x+2=4^2-8 \times 4+2=-14\]
.The turning or stationary point is
\[(4,-14)\]
\[\frac{d^2y}{dx^2}=2 \gt 0\]
, so the point is a minimum. 