We are given two circles, one inside the other, touching tangentially at the bottom, with a vertical line AB tangential to the smaller, a chord to the larger as shown.
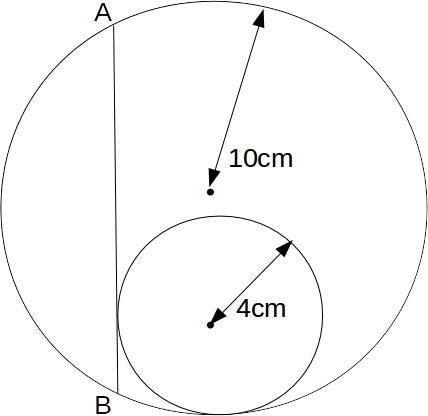
We can find the length of the line AB using Pythagoras Theorem. Draw a horizontal line from the center of the large circle to the line AB. The triangle ABC is right angled.
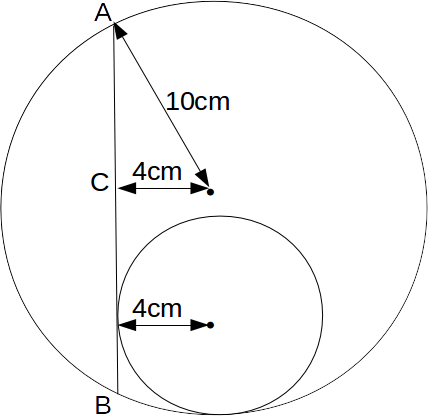
\[CA=\sqrt{10^2-4^2}= \sqrt{84}c=2 \sqrt{21}\]
cm
Then
\[AB=2AC=4 \sqrt{21}cm\]
.



