Finding the angle between vertices in a three dimensional solid can be tricky. It often helps to construct a triangle between the relevant vertices. Then it is often possible to use trigonometry. Consider the hexagonal pyramid below.
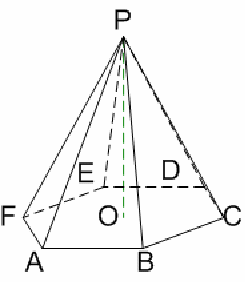
The base is a regular pyramid and all the sides are the same length, 2cm. The pyramid is 5 cm high.
We want to find the angle
for which we need to find the length
The base of the pyramid is shown below.
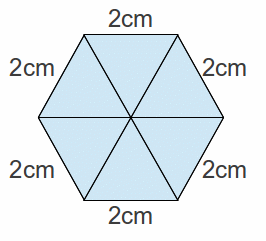
We may cut the base up into six equilateral triangles, so that each angle is 60 and each length is 2 cm The length
(O is the centre of the base so FOC is a straight line) is then 4 cm and we may construct the triangle below.
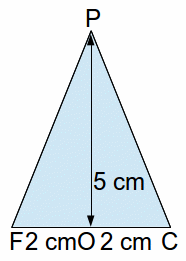
The angle
is twice the angle
The triangle
is right angled so
and
Finding the angle
is trickier. We have to find the slant height
and the distance
From the triangle above, Pythagoras Theorem gives
W can draw the triangle below to find
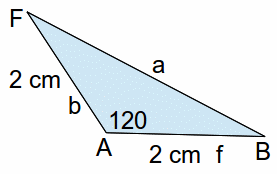
We can find the distance AB using the cosine rule
The triangle
is then
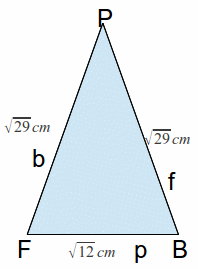
We can findusing the cosine rule.
