Maximising and Minimising Expressions

Suppose we want to find the maximum distance between two points. We might know where the two point are, but it is in the nature of measurements that they are never exact.

A is at 2 to the nearest whole number. This means is must be closer to 2 than any other whole number, but this means it can be anywhere between 1.5 (halfway between 1 and 2) and 2.5 (halfway between 2 and 3), and B is at 5 to the nearest whole number but this means it can be anywhere between 4.5 and 5.5. From the diagram above the

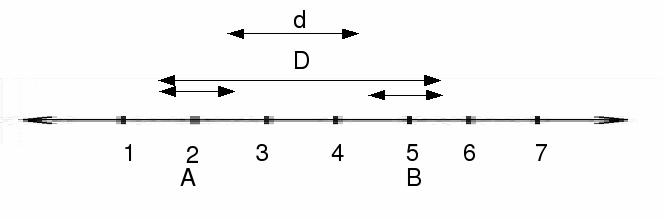
maximum possible distance between A and B is 5.5-1.5=4

minimum possible distance between A and B is 4.5-2.5=2

In general to find the maximum possible value ofwe find

To find the minimum possible value ofwe find

TO FIND THE MAXIMUM POSSIBLE VALUE OFWE DO NOT FIND

TO FIND THE MINIMUM POSSIBLE VALUE OFWE DO NOT FIND

The above may seem counter intuitive. So is this:

To find the maximum possible value offind

To find the minimum possible value ofwe find

Examples:

If x=2.5 to the nearest 0.1 and y is 3.4 to the nearest 0.1 find the maximum and minimum possible values of

the maximum and minimum possible values ofare 2.45 and 2.55 respectively and the maximum and minimum possible values ofare 3.35 and 3.45 respectively.

to 4 d.p.

To 4 d.p.