60 children go to school. There are various methods they use – they may walk, go by car, bus or train. The statistics are in the following table.
|
Method of Going to School |
Frequency |
Angle |
|
Walk |
21 |
|
|
Car |
15 |
|
|
Bus |
20 |
|
|
Train |
4 |
|
|
Total |
60 |
360 |
Because it is for a pie chart, the angles have to add to 360 o . The frequencies add to 60. If we multiply the total of the frequencies by 6 do in fact add up to 360.
In general to calculate the angles we find the scale factor between the Frequency and Angles columns by looking at the Total row and finding the scale factor. The finished table is shown below
|
Method od Going to School |
Frequency |
Angle |
|
Walk |
21 |
126 |
|
Car |
15 |
90 |
|
Bus |
20 |
120 |
|
Train |
4 |
24 |
|
Total |
60 |
360 |
We can always do this – find the scale factor from the shares column to the £ (or whatever is actually being shared out column) then multiply the shares by the scale factor to get the answers.
Example:
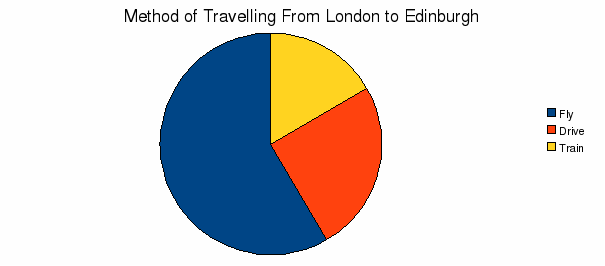
12 people travel from London to Edinburgh. 7 fly, 3 drive and 2 take the train. Sketch a pie chart.
|
Method |
Frequency |
Angle |
|
Fly |
7 |
210 |
|
Drive |
3 |
90 |
|
Train |
2 |
60 |
|
Total |
12 |
360 |
T^he scale factor from the Frequency to the Angle column is 30 – worked out from the bottom row - so multiply the frequency column by 30 to get the Angle column. We can now draw the pie Chart.