The ambiguous case arises when using the Sine Rule to find an angle in a triangle. It occurs because the Sin function is symmetric about 90°, so that![]()
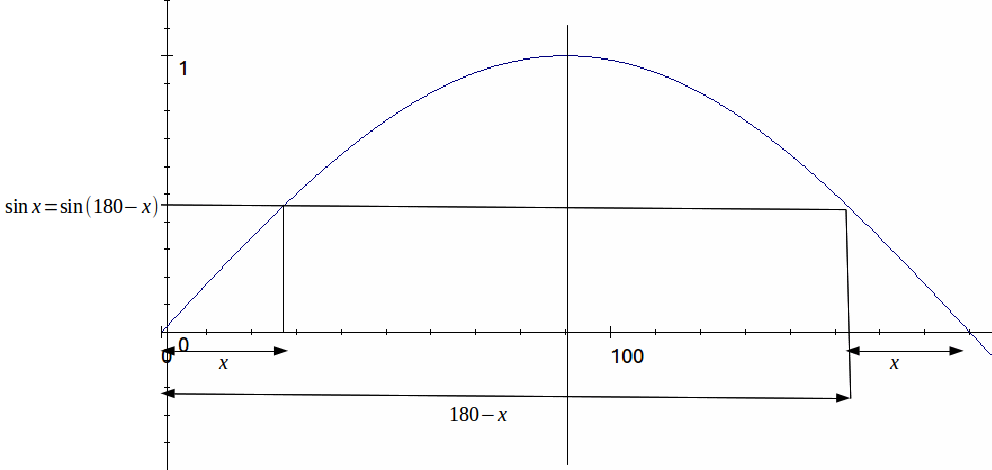
When we solve for![]() there is an acute solution,
there is an acute solution,![]() and an obtuse solution,
and an obtuse solution,![]()
Example: Find the angle A in the triangle below.
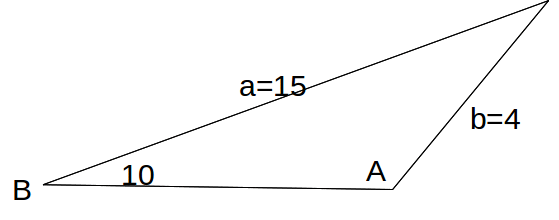
The Sine Rule states![]()
![]()
Then![]()
This is obviously wrong since A is obtuse.
In fact![]()
