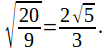Absolute value equations typically do not have single solutions, or even a set of solutions which can be listed. Typically, the solution describes a curve in the complex plane. To take a very simple example, the equation
has the solution given in polar form as
or in cartesian form as
with
Often it is easiest to find the solution in cartesian form by substituting z=x+iy and collecting real and imaginary terms, squaring and adding them to give a real number.
Example: Solve
Write the equation as
and multiply by
to give
(1)
Now substitute z=x+iy.
Substitute these two expressions into (1) to obtain
Square both sides to give
Now multiply out the brackets and collect like terms.
Divide by 3 and complete the square.
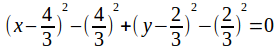
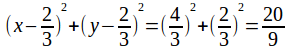
This is the equation of a circle with centre
and radius