The product principle applies to counting problems and is a way of counting all possible outcomes, when choices are made in sequence, with all choices being possible at each stage. Suppose for example that a man is to travel from town A to town D via the intermediate towns B and C.
From town A there are a possible routes to town B.
From town B there are b possible routes to town C.
From town C there are c possible routes to town D.
Then there are abc possible routes from town A to town D calling at the intermediate towns B and C.
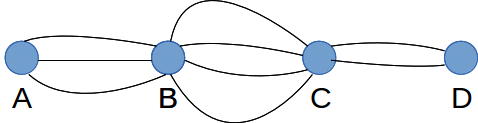
The diagram above shows three routes from A to B, four routes from B to C and two routes from C to D, so there are 3*4*2=24 routes from A to D calling at B and C.
Obviously the product principle can be extended to any number of towns and routes between each town.
Formally the product principle states:
If there are m ways of performing an operation and for each of these there are n ways of performing a second independent operation, there are mn different ways of performing the two operations.
